Affine transformation

Affine Transformation

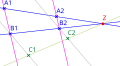
An affine transformation is a function between affine spaces which preserves points, straight lines, and planes. Sets of parallel lines remain parallel after an affine transformation. An affine transformation can be constructed using a linear transformation followed by a translation.

Affine transformations are fundamental in computer graphics, image processing, and computer vision, as they can represent any combination of translation, scaling, rotation, and shearing.

Mathematical Definition

An affine transformation in two-dimensional space can be represented by the equation:

\( \mathbf{y} = \mathbf{A} \mathbf{x} + \mathbf{b} \)

where \( \mathbf{A} \) is a linear transformation matrix, \( \mathbf{x} \) is the input vector, \( \mathbf{b} \) is the translation vector, and \( \mathbf{y} \) is the output vector.

In matrix form, this can be written as:

\[

\begin{bmatrix} y_1 \\ y_2 \\ 1 \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & b_1 \\ a_{21} & a_{22} & b_2 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ 1 \end{bmatrix} \]

Types of Affine Transformations

• Translation: Shifts every point of a shape in the same direction by the same distance.
• Scaling: Enlarges or diminishes objects; the scale factor is the same in all directions.
• Rotation: Rotates objects around a fixed point.
• Shearing: Slants the shape of an object.
• Reflection: Flips objects over a line.

Properties

Affine transformations preserve:

• Collinearity: Points that lie on a line continue to be collinear.
• Ratios of distances: The midpoint of a line segment remains the midpoint after transformation.
• Parallelism: Parallel lines remain parallel.

Applications

Affine transformations are widely used in:

• Computer graphics: For rendering images and animations.
• Image processing: For image registration and alignment.
• Robotics: For coordinate transformations and motion planning.
• Geometric modeling: For transforming geometric shapes.

Related Pages

• Linear transformation
• Matrix (mathematics)
• Euclidean transformation
• Projective transformation

Gallery

• 

  Fractal fern created using affine transformations.

• 

  Video illustrating affine transformations.

• 

  Identity transformation on a checkerboard.

• 

  Reflection transformation on a checkerboard.

• 

  Scaling transformation on a checkerboard.

• 

  Rotation transformation on a checkerboard.

• 

  Shearing transformation on a checkerboard.

• White on black circle image 256 by 256.png

  Original circle image.

• Affine transform sheared circle.png

  Sheared circle image.

• 

  Central dilation example.