Bifurcation theory

Bifurcation theory is a branch of mathematics that studies changes in the qualitative or topological structure of a given family of mathematical models. It is a key concept in the field of dynamical systems, where it describes how the structure of these systems changes as a parameter is varied. Bifurcations can lead to dramatic changes in the behavior of a system, including the appearance or disappearance of equilibria, the change in stability of an equilibrium, or the birth of chaotic behavior.

Overview

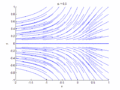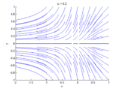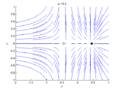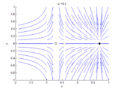
In the context of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations are classified into various types, including but not limited to, saddle-node bifurcation, transcritical bifurcation, pitchfork bifurcation, and Hopf bifurcation. Each type has its own characteristic changes in the system's dynamics.

Types of Bifurcations

Saddle-Node Bifurcation

In a saddle-node bifurcation, two fixed points (one stable and one unstable) collide and annihilate each other as a parameter is varied. This type of bifurcation is also known as a fold bifurcation.

Transcritical Bifurcation

A transcritical bifurcation involves the exchange of stability between two fixed points as a parameter is varied. In this scenario, a stable and an unstable point intersect and swap their stabilities.

Pitchfork Bifurcation

Pitchfork bifurcation can be either supercritical or subcritical and involves one fixed point becoming unstable and giving rise to two new stable fixed points (supercritical) or two unstable fixed points (subcritical).

Hopf Bifurcation

In a Hopf bifurcation, a fixed point loses stability as a pair of complex conjugate eigenvalues cross the imaginary axis in the complex plane, leading to the creation of a limit cycle.

Applications

Bifurcation theory has wide-ranging applications across various fields including biology, where it is used to understand phenomena such as the heartbeat and neural activity; in engineering for the analysis of systems stability; and in economics for modeling market equilibria and transitions.

Mathematical Formulation

The mathematical study of bifurcations is a complex area that involves differential equations, fixed point theory, and linear algebra, among other mathematical disciplines. The normal form theory and center manifold theory are two of the main tools used in the analysis of bifurcations.

See Also

• Dynamical systems
• Chaos theory
• Stability theory

References

   This article is a mathematics-related stub. You can help WikiMD by expanding it!

Bifurcation_theory

• 

  Saddlenode

• 

  Chaos order chaos

• 

  Homoclinic bifurcation

• 

  Hopf and homoclinic bifurcation

• 

  Hopf and homoclinic bifurcation 2

• 

  Hopf bifurcation, with limit cycle up to order 3-2