Dijkstra's algorithm
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
Overview
Dijkstra's algorithm is used to find the shortest path from a starting node (source) to a target node in a weighted graph. The graph can be directed or undirected, but the weights on the edges must be non-negative. The algorithm works by iteratively selecting the node with the smallest tentative distance, updating the distances of its adjacent nodes, and marking the selected node as "visited."
Algorithm Description
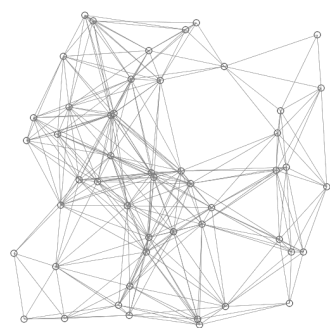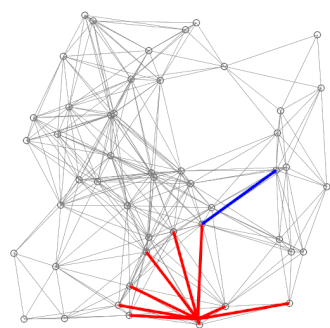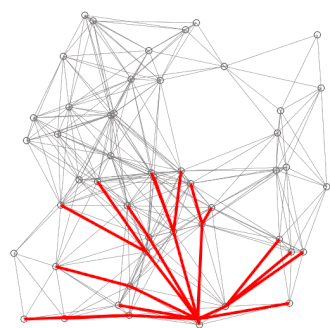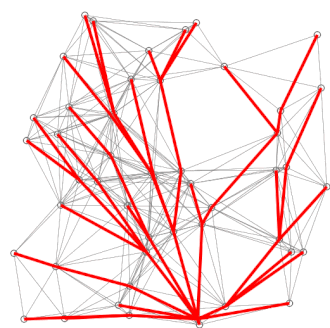
The algorithm maintains a set of nodes whose shortest distance from the source is known and a set of nodes whose shortest distance is not yet known. Initially, the distance to the source node is set to zero, and the distance to all other nodes is set to infinity. The algorithm proceeds as follows:
- Initialize the distance to the source node to 0 and all other nodes to infinity.
- Set the source node as the current node.
- For the current node, consider all of its unvisited neighbors and calculate their tentative distances through the current node. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one.
- After considering all of the unvisited neighbors of the current node, mark the current node as visited. A visited node will not be checked again.
- If the destination node has been marked visited (when planning a route between two specific nodes) or if the smallest tentative distance among the nodes in the unvisited set is infinity (when there is no connection between the source and remaining unvisited nodes), then stop. The algorithm has finished.
- Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new "current node," and go back to step 3.
Pseudocode
The following is a high-level pseudocode description of Dijkstra's algorithm:
``` function Dijkstra(Graph, source):
dist[source] ← 0
for each vertex v in Graph:
if v ≠ source:
dist[v] ← infinity
add v to Q
while Q is not empty:
u ← vertex in Q with min dist[u]
remove u from Q
for each neighbor v of u:
alt ← dist[u] + length(u, v)
if alt < dist[v]:
dist[v] ← alt
prev[v] ← u
return dist, prev
```
Applications
Dijkstra's algorithm is widely used in network routing protocols, such as Open Shortest Path First (OSPF) and Intermediate System to Intermediate System (IS-IS). It is also used in various applications like geographic information systems (GIS) for finding the shortest path between locations on a map.
Limitations
While Dijkstra's algorithm is efficient for graphs with non-negative weights, it does not work correctly with graphs that contain negative weight edges. For such graphs, algorithms like the Bellman-Ford algorithm are used.
Related Pages
See Also
References
External Links
Transform your life with W8MD's budget GLP-1 injections from $125.
W8MD offers a medical weight loss program to lose weight in Philadelphia. Our physician-supervised medical weight loss provides:
- Most insurances accepted or discounted self-pay rates. We will obtain insurance prior authorizations if needed.
- Generic GLP1 weight loss injections from $125 for the starting dose.
- Also offer prescription weight loss medications including Phentermine, Qsymia, Diethylpropion, Contrave etc.
NYC weight loss doctor appointments
Start your NYC weight loss journey today at our NYC medical weight loss and Philadelphia medical weight loss clinics.
- Call 718-946-5500 to lose weight in NYC or for medical weight loss in Philadelphia 215-676-2334.
- Tags:NYC medical weight loss, Philadelphia lose weight Zepbound NYC, Budget GLP1 weight loss injections, Wegovy Philadelphia, Wegovy NYC, Philadelphia medical weight loss, Brookly weight loss and Wegovy NYC
|
WikiMD's Wellness Encyclopedia |
| Let Food Be Thy Medicine Medicine Thy Food - Hippocrates |
Medical Disclaimer: WikiMD is not a substitute for professional medical advice. The information on WikiMD is provided as an information resource only, may be incorrect, outdated or misleading, and is not to be used or relied on for any diagnostic or treatment purposes. Please consult your health care provider before making any healthcare decisions or for guidance about a specific medical condition. WikiMD expressly disclaims responsibility, and shall have no liability, for any damages, loss, injury, or liability whatsoever suffered as a result of your reliance on the information contained in this site. By visiting this site you agree to the foregoing terms and conditions, which may from time to time be changed or supplemented by WikiMD. If you do not agree to the foregoing terms and conditions, you should not enter or use this site. See full disclaimer.
Credits:Most images are courtesy of Wikimedia commons, and templates, categories Wikipedia, licensed under CC BY SA or similar.
Contributors: Prab R. Tumpati, MD