Ellipse

A type of conic section

An ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. It is one of the four types of conic sections, the others being the parabola, hyperbola, and the circle, which is a special case of the ellipse.

Definition

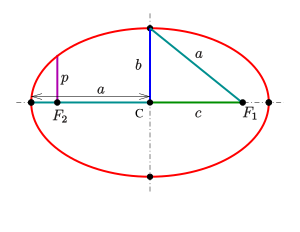
An ellipse can be defined as the set of all points in a plane such that the sum of the distances from two fixed points, called the foci (singular: focus), is constant. This constant is greater than the distance between the foci.

Diagram of an ellipse as a conic section

Properties

Axes

The longest diameter of the ellipse is called the major axis, and the shortest diameter is the minor axis. The major and minor axes are perpendicular to each other and intersect at the center of the ellipse.

Eccentricity

The eccentricity of an ellipse is a measure of how much it deviates from being circular. It is defined as the ratio of the distance between the foci to the length of the major axis. An ellipse with an eccentricity of 0 is a circle.

Diagram showing the eccentricity of an ellipse

Foci

The foci of an ellipse are two special points located along the major axis, equidistant from the center. The sum of the distances from any point on the ellipse to the foci is constant.

Diagram showing the definition of an ellipse with foci

Directrix

An ellipse can also be defined in terms of a directrix and eccentricity. For each focus, there is a corresponding directrix, and the ratio of the distance of any point on the ellipse to a focus and to the corresponding directrix is constant and equal to the eccentricity.

Diagram showing the directrix of an ellipse

Parametric Representation

An ellipse can be represented parametrically by the equations:

\[ x = a \cos(t) \\ y = b \sin(t) \]

where \(a\) and \(b\) are the semi-major and semi-minor axes, respectively, and \(t\) is the parameter.

Parametric representation of an ellipse

Area and Perimeter

The area \(A\) of an ellipse is given by the formula:

\[ A = \pi ab \]

where \(a\) and \(b\) are the semi-major and semi-minor axes, respectively.

The perimeter \(P\) of an ellipse does not have a simple closed-form expression, but it can be approximated by Ramanujan's formula:

\[ P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \]

Applications

Ellipses have many applications in physics, engineering, and astronomy. For example, the orbits of planets and satellites are often elliptical, with the central body located at one of the foci.

General diagram of an ellipse

Related Pages

• Conic section
• Circle
• Parabola
• Hyperbola