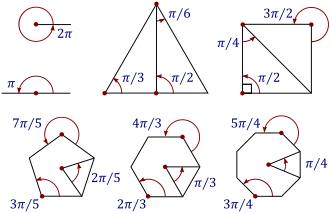
Radian

Radian-common

Radian is a unit of measure used in the field of geometry to quantify angles. It is the standard unit of angular measure in the International System of Units (SI), and it is used widely in many areas of mathematics, physics, and engineering. The radian is defined as the angle created at the center of a circle by an arc whose length is equal to the radius of the circle. This definition implies that a full circle encompasses \(2\pi\) radians, which corresponds to 360 degrees, making one radian equal to approximately 57.2958 degrees.

Definition

The radian is defined based on the radius of a circle. Specifically, if the length of an arc of a circle is equal to the radius of that circle, then the angle subtended by that arc at the center of the circle is one radian. Mathematically, this can be expressed as \(1 \, \text{radian} = \frac{\text{arc length}}{\text{radius}}\). This relationship highlights the radian's nature as a ratio and thus a dimensionless unit, which sets it apart from degrees, a unit also used to measure angles but defined arbitrarily as 1/360 of a circle.

Conversion between radians and degrees

To convert between radians and degrees, one can use the fact that \(360^\circ\) is equivalent to \(2\pi\) radians. Therefore, to convert degrees to radians, one multiplies the number of degrees by \(\frac{\pi}{180}\), and to convert radians to degrees, one multiplies the number of radians by \(\frac{180}{\pi}\).

Usage

Radians are widely used in various branches of mathematics, including trigonometry, calculus, and linear algebra, due to their natural properties that simplify many types of calculations. For example, the derivatives of trigonometric functions are simpler when the functions' arguments are given in radians. In physics, radians are used to describe angular velocities and accelerations, among other quantities. Engineers also use radians in the design and analysis of mechanisms and systems that involve rotation or oscillation.

Advantages

One of the main advantages of using radians is that they allow for more straightforward and intuitive equations and formulas. For instance, in calculus, the derivative of the sine function is cos(x) only when x is measured in radians. This simplicity extends to the Taylor series expansions of trigonometric functions and the solutions to many differential equations.

See also

• Degree (angle)
• Circle
• Trigonometry
• Calculus

This article is a medical stub. You can help WikiMD by expanding it!
Most recent articles Ongoing trials	Wikipedia