Simple harmonic motion

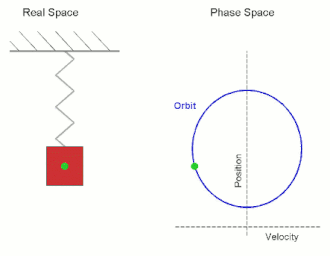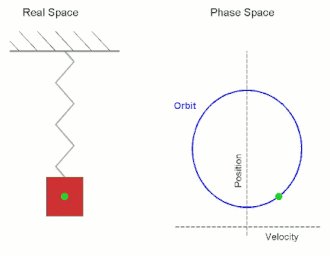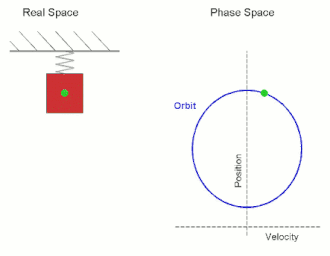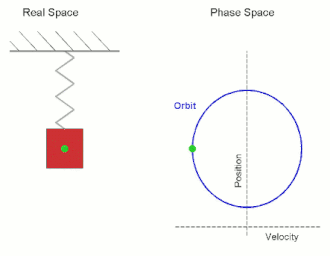
Simple Harmonic Motion Orbit

Animated-mass-spring

ลูกตุ้มธรรมชาติ

Scotch yoke animation

Simple Harmonic Motion (SHM) is a type of periodic motion or oscillation motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement. SHM can serve as a mathematical model for a variety of motions, such as the oscillation of a spring or the pendulum of a clock.

Definition

In simple harmonic motion, the displacement x of the particle from the equilibrium position is described by the equation:

\[ x(t) = A \cos(\omega t + \phi) \]

where:

• A is the amplitude of the oscillation - the maximum displacement from the equilibrium position.
• \(\omega\) is the angular frequency of the oscillation, which determines how many oscillations occur in a unit of time.
• t is the time.
• \(\phi\) is the phase of the oscillation at t = 0.

The velocity v and acceleration a of the particle can be derived from the displacement as:

\[ v(t) = -A\omega \sin(\omega t + \phi) \] \[ a(t) = -A\omega^2 \cos(\omega t + \phi) \]

The acceleration is thus also directly proportional to the displacement but in the opposite direction, which characterizes SHM.

Characteristics

• Periodic Motion: SHM repeats itself in equal intervals of time known as the period (T).
• Restoring Force: The force that brings the system back to its equilibrium position is always directed opposite to the displacement.
• Energy Conservation: In SHM, energy is conserved, oscillating between kinetic energy and potential energy.

Examples

• A mass attached to a spring on a frictionless surface.
• A simple pendulum, for small angles of displacement.
• The motion of a diatomic molecule.

Mathematical Analysis

The period T of simple harmonic motion is given by:

\[ T = 2\pi\sqrt{\frac{m}{k}} \]

where m is the mass of the oscillating object and k is the spring constant for a mass-spring system, or the gravitational constant over the length of the pendulum in the case of a simple pendulum.

The frequency f is the reciprocal of the period (T):

\[ f = \frac{1}{T} \]

Applications

SHM is foundational in the study of waves and vibrations, and has applications in various fields including engineering, physics, and even music. Understanding SHM is crucial for the design of structures that must withstand vibrational forces, such as buildings in earthquake-prone areas, and for the analysis of sound waves.

See Also

• Harmonic oscillator
• Pendulum
• Wave motion

   This article is a physics-related stub. You can help WikiMD by expanding it!